Project 2: Train Your Own Artificial Neural Network
Due: Tues, Oct 20 (11:59 PM)
This project involves training your own neural networks. In the first part, you will implement back-propagation and gradient descent yourself on a fully-connected feedforward neural network. In the second part, you will use Caffe, which you have already installed in the first project, to train a more sophisticated convolutional neural network.
Dataset
For this project, we will look at classifying handwritten digits from the MNIST dataset. You can start by downloading and extracting the 4 datasets from the MNIST website. These consist of images and labels for both the training and testing datasets. As a reminder, in machine learning, frequently one trains on one dataset, and tests on an independent dataset. Usually in the end performance is reported on the test dataset, because repeatedly fitting parameters to the same training dataset can result in overfitting, which manifests as artificially low training errors.
The dataset is in a custom binary format. You can load it into a programming language of your choice by using a loader. There are available loaders for Python (which is slightly modified to use floating point arrays from the blog post where it is documented), MATLAB, or C.
Part 1: Building Your Own Neural Network from Scratch
In this part of the project, you will implement your own fully-connected feedforward neural network. The benefit of doing this is that you will understand in detail how neural networks work and are trained. You will implement a neural network with the following structure:
A multi-layer feedforward neural network. Image from Wikipedia user Paskari.
Your task is to implement the following:
- An evaluation method that evaluates the output of the network, given the input array (in our case, an image), and the weights of the network.
- An error function (also known as a loss function) that evaluates the predicted output from the network against the ground truth label, for a subset of either the training or testing images.
- A training method that calls two other methods in a loop until a maximum iteration count is reached:
- Backpropagation, which finds the partial derivatives of the output energy with respect to each weight in the network. See also the backpropagation tutorial which we covered in class.
- Gradient descent, which adjusts the parameters of the network to decrease the energy function. For this assignment it suffices to use ordinary gradient descent which evaluates the gradient of the error function over all images in the training set. However, you can obtain a few points of extra credit by using stochastic gradient descent, and comparing the convergence rates of ordinary and stochastic gradient descent.
General suggestions:
- If one uses the languages MATLAB or Python, then to obtain reasonable efficiency, it will be necessary to express the operation that computes the output of a current layer as an array operation. Specifically, one can compute the output vector L(i) of a layer as the activation function f applied to the matrix product W(i)L(i-1), where W is a rectangular weight matrix storing the weights for all connections between layers i-1 and i.
- To include a bias term, we suggest to add to each layer (including the input layer) a "virtual" neuron whose output is always 1. Then the same matrix computation above will now include a bias term. With this approach, the value for the biases are stored in the weight matrix, and can be updated by backpropagation in the same manner as all other weights.
- One can subsample the training dataset: for example, one can choose the first few thousand images from it. This will decrease accuracy but also decrease training time during debugging stages.
- For each training image, one can downsample the image by say decreasing the width and height both by a factor of d = 2. This will further decrease training times. One can turn the resulting smaller image into an input to the network by flattening it (in MATLAB,
I(:), or in Python, I.flatten()).
- One must also choose an error function. I used a simple sum of squared differences between the network's output and the target output, which was a vector that contains all zeros except a one in the location of the labelled correct digit.
Parameters:
- One must choose an activation function for each layer of the network, and the number of hidden layers and hidden neurons.
- I found I obtained a test accuracy of around 80% by using a 3 layer architecture, with sigmoid activation functions everywhere, a 14x14 input image, 200 hidden neurons, and a 10 long output layer (with one neuron for each digit), and running on only part of the training set. This performance is quite bad though: by fine-tuning parameters and running on the full training set, you should be able to get better performance!
What to submit for Part 1:
- Your code
- Report your test accuracy and network architecture.
- Which architecture gives the best performance? Do you find using 0, 1, or more hidden layers gives the best result?
Part 2: Training More Sophisticated Networks with Caffe
The algorithms are no different to train significantly larger networks, or networks using other weight matrices such as those created by convolutions. One simply uses backpropagation and stochastic gradient descent. However, engineering efficient code for such "deep learning" is a practical challenge, which is why people use libraries such as Caffe or Torch.
In Part 2 you will be using Caffe to see if you can improve the performance over the small neural network you built in Part 1.
Installation and Setup of Caffe
The program environment can use your already installed Caffe package and make some slight modifications:
- We suggest to install the Anaconda Python distribution, which provides most of the necessary packages.
- You can open IPython in the same manner as the first assignment, download this example of digit recognition, and modify it. More basic tutorials for Caffe are also available.
Your Tasks
- Visualize the test results for the MNIST digit training images and plot the train loss and test accuracy figure as in the example of digit recognition:
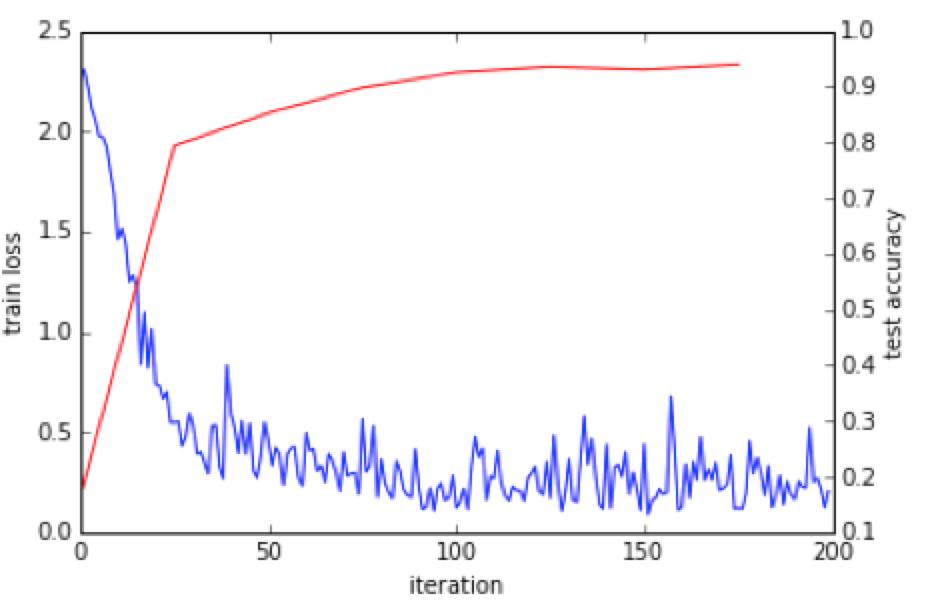
- Report the overall test accuracy, and experiment to configure the network to achieve maximum accuracy. Experiment with modifying the neural network activation functions, pooling sizes, convolution stencil sizes, and so forth. You can also try different learning rate, different gradient descent methods and other setting parameters, so see if it improves test accuracy.
Policies
Feel free to collaborate on solving the problem but write your code individually.
Submission
Submit your assignment in a zip file named yourname_project2.zip. Please include your source code from part 1. Also, include a document named writeup.doc, describing the best accuracy you achieved in parts 1 and 2, the neural network architectures you used to achieve this accuracy, and the answers to the last question of part 1.
Finally submit your zip to UVA Collab.


