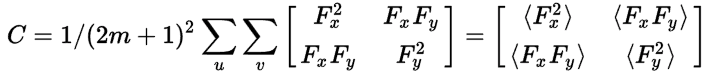Project 1: Edge and corner detector

• Python: User guide for the scikit-image image processing library
• Python: Array facility (numpy) documentation: user guide, array objects
• Python: A brief tutorial on loading an image, showing it, and applying a convolution.
• Python: A longer tutorial including some introduction to the language, data types, functions, the standard library, the array facility (numpy), and some image processing.
• MATLAB: A short introduction
• MATLAB: A longer tutorial
• MATLAB: Some image processing commands from the previous version of this course.

Assignment Overview

Left: an input image. Center: result of Canny edge detection. Right: Result of corner detection.

Canny edge detector (65%)

• Compute smoothed gradients:
  
  
  1. Load an image, convert it to float format, and extract its luminance as a 2D array.
     
     
  2. Find the x and y components Fx and Fy of the gradient of the image after smoothing with a Gaussian (for the Gaussian, you can use σ = 1). As discussed in the lecture, there are two ways to go about doing this: either (A) smooth with a Gaussian using a convolution, followed by taking the gradient; or (B) convolve with the x and y derivatives of the Gaussian.
     
     Please use one of the convolution routines (e.g. scipy.signal.convolve2d or scipy.ndimage.filters.convolve), as opposed to specialized methods for Gaussian filtering, because this will give you practice using convolutions.
     
     
  3. At each pixel, compute the edge strength F (the magnitude of the gradient), and the edge orientation D = atan(Fy/Fx).
     
     
• Nonmaximum suppression:
  
  Create a "thinned edge image" I[y, x] as follows:
  
  
  1. For each pixel, find the direction D* in (0, π/4, π/2, 3π/4) that is closest to the orientation D at that pixel.
  2. If the edge strength F[y, x] is smaller than at least one of its neighbors along the direction D*, set I[y, x] to zero, otherwise, set I[y, x] to F[y, x]. Note: Make a copy of the edge strength array before thinning, and perform comparisons on the copy, so that you are not writing to the same array that you are making comparisons on.
     
     
  Note: After thinning, your "thinned edge image" should not have thick edges any more (so edges should not be more than 1 pixel wide).
  
  
• Hysteresis thresholding:
  
  
  1. We are given two thresholds: T_low, and T_high.
  2. Mark pixels as "definitely not edge" if less than T_low.
  3. Mark pixels as "strong edge" if greater than T_high.
  4. Mark pixels as "weak edge" if within [T_low, T_high].
  5. Strong pixels are definitely part of the edge. Weak pixels are debatable.
  6. Only include weak pixels that are connected in a chain to a strong pixel. How to do this?
     • Visit pixels in chains starting from the strong pixels. For each strong pixel, recursively visit the weak pixels that are in the 8 connected neighborhood around the strong pixel, and label those also as strong (and as edge).
     • Label as "not edge" any weak pixels that are not visited by this process.
     • Hint: This is really a connected components algorithm, which can be solved by depth first search. Make sure to not revisit pixels when performing your depth first search!

Corner detector (35%)

• Filtered gradient: Compute x and y gradients Fx and Fy, the same as in the Canny edge detector.
  
  
• Find corners: For each pixel (x, y), look in a window of size 2m+1 x 2m+1 around the pixel (you can use say m = 4). Accumulate over this window the covariance matrix C, which contains the average of the products of x and y gradients:
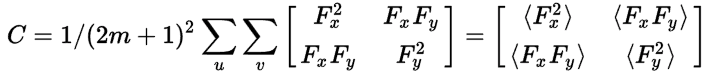
  Here (u, v) are the coordinates within the window: u = -m, ..., m, and v = -m, ..., m, the brackets (< and >) indicate a spatial averaging operation, and the gradients Fx and Fy on the right hand side of the above equation are read from the locations (x + u, y + v).
  
  Compute the smaller eigenvalue, e, of C, which is the "corner response" (note that the original Harris corner detector paper uses a different and faster formula of e = Determinant(C)-kTrace(C)², where k is a small constant such as 0.04, so you can alternatively use that formulation instead if you like). In Python, see the command numpy.linalg.eig, which computes the eigenvalues. In MATLAB, use the eig command. Save all pixels at which the corner response e is greater than a corner threshold T into a list L.
  
  
• Nonmaximum suppression: Sort L in decreasing order of the corner response e. See numpy.sort and numpy.argsort, or the Python built-in function sorted. For each point p, remove all points in the 8-connected neighborhood of p that occur later in the list L.
  

Policies

Submission