
| Contents 1. Introduction 2. Verlet Integration 3. Constraints 4. Interactions Between Hair Segments 5. Interaction Between Quads and Vertices 6. Interpolation 7. Static Links 8. Results 9. Discussion |
I am Connelly Barnes, and I implemented the paper "A Practical Model for Hair Mutual Interaction" by Chang, Jin, and Yu. The paper is available online under the animation section of [1]. My presentation is available in PDF format, and my source code is available (licence: public domain, includes executable). I also made a movie [2] of my results.
I used the Verlet integration [3] approach described in the article "Advanced Character Physics" by Thomas Jakobsen [4]. The primary advantage of this approach is that one need not use Lagrange's equations or calculate velocity changes due to collisions -- instead, the motion of the system is described by particles in rectangular coordinates, and changes in velocity are effected by placing position constraints on the relative positions of the particles. Also, the method is rather fast: the video on this page was captured from my hair simulation in realtime (~15 frames/sec).
For my hair simulation, I used a 12x6 rectangular grid specified in polar coordinates on a spherical "scalp." Each hair has length one and contains 20 joints. The hairs initially extend straight outward from the scalp in the r direction. In each step of the simulation, the forces on each particle are accumulated, applied during the Verlet integration update, and then the constraint "relaxation" process is called.
In the simplest case, the only forces on the particles are gravity and wind drag:
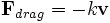
With the Verlet integrator, we always store the current position and the previous position of each joint. The Verlet integration update rule is:
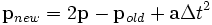
The velocity of each joint is never explicitly stored; instead it is recomputed whenever it is needed from the current position:
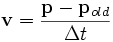
One can thus see how the Verlet integration is derived: the velocity times the change in time is added to the current position, yielding the Verlet update rule. I ran into trouble when using adaptive timestepping, so I would recommend a fixed timestep.
After performing the Verlet update, the new joint positions may be invalid. Assume that the joints are connected with segments, and that each segment has length L. We wish to constrain the hair to behave as an n-body pendulum. To do this, we loop over the segments connecting joints, starting from the segment closest to the scalp. For the first segment, we modify the position of the 2nd joint so that it is exactly L distance from the first joint. The first joint is never moved by the constraint process, as it is anchored to the scalp. For the next segment, we have two adjacent joints a and b which are presumably do not have a distance L between them -- that is, they violate the constraint. We therefore enforce the position constraint via Jakobsen's position update rule:
vec3 delta = b - a
float d = length(delta)
delta *= 0.5 * (L - d) / d
a -= delta
b += delta
We continue down the hair chain until we reach the last segment, which is at the tip of the hair.
Next we wish to push hairs out of the scalp sphere. I did this by looping over each segment on the hair, finding the point on the segment closest to the center of the sphere; if that point is inside the sphere, push it to the surface of the sphere with a normalize() call, and then apply this same translation to both of the endpoints of the segment. If the segment is inside the sphere, then this process will push it so that it ends up tangent to the sphere (unless the point on the segment closest to the center of the sphere was an endpoint, in which case the segment ends up touching the sphere at one end).
Notice that we do two separate loops over the segments to enforce the segment-length and the segment-not-in-sphere constraints, and in each case when we "fix" one constraint we will usually end up violating other constraints. This is acceptable, as the constraints tend to "relax" over time so that all constraints are satisfied. With a simulation framerate of 40 frames/sec, I found that in each frame, for each hair, I needed to repeat this constraint process 20 times. If the constraint process is repeated too few times, then the hairs stretch as the segment-length constraints are violated, and the hairs may push slightly into the sphere.
The next stage of the simulation requires that we determine collisions between a large number of line segments -- two segments are deemed to collide if the minimum distance between them is less than the hair diameter. The first stage of collision detection is called "broadphase;" the goal here is to determine as quickly as possible which pairs of objects are potentially intersecting. One then performs more expensive computations in "narrowphase" collision detection to see which of the given pairs actually intersects. One can use a naive O(n2) algorithm for broadphase or an octree. I used a simple algorithm: retrieve axis-aligned bounding boxes (AABBs) for all objects, sort all of the objects by minimum bounding box x coordinate, then for each index i of the objects in the sorted list, try j=i+1, i+2, ..., and for each (i, j) if the two object's bounding boxes collide then add the object to the collision set and if object j's minimum is greater than object i's maximum then stop the loop over j (and try the next i index). I benchmarked this algorithm against the octree and it outperformed the octree for the cases which I cared about.
Now we can determine which hair segments collide. One can calculate AABBs for each hair segment or hair, throw these into the broadphase collision algorithm, and for each potentially colliding pair, determine the segment-segment distance. If the distance is less than a threshold, add a spring force
Where x is the difference between the threshold and the actual distance, and the force is applied along the vector which gives the shortest distance between the segments. I initially used calculus to determine the shortest distance between line segments; however this was too slow, so I simply divided each segment into 3 points and used the shortest distance between points as an approximation.
If only the previous sections are implemented, then one can produce a reasonable looking simulation for hair on a brush. However, human hair tends to form layers, so the paper by Chang et al suggests placing faces between adjacent guide hairs, and then colliding all hair vertices with these faces. In theory, we simply find the minimal distance between each face and each hair vertex, check whether this is below the hair radius plus the face's "radius," and if so, apply a spring force. In practice I formed the layers out of quads, used the same broadphase collision detection as from the previous section, and a quad-vertex minimal distance computation to determine the distance and direction in which the spring force should be applied. I divided the force applied to the quad equally among the four quad vertices. I also only used "horizontal" layers (one can join adjacent guide hairs on the grid horizontally and/or vertically with faces, and I only joined them horizontally). This allows the hairs to move somewhat freely around the z axis, however, the effect looks decent when interpolated hairs are added, and the layers do "bunch up" so that the hair layers do not lie flat; they have volume.
The guide hairs are not "dense" enough to appear realistic if rendered alone. In my simulation, the number of segments per guide hair is 20, and this gives a reasonable appearance of a smooth curve. However, a cubic Hermite spline can be used to subdivide the guide hair curves if desired [5]. To add to the density of the hair, I used bilinear interpolation. For every 4 guide hairs (the roots are arranged in a "rectangle" on the scalp), I rendered a 5x5 grid of rendered hairs. Normally one would space the interpolated hairs equally, with interpolation parameters such as t = 0, 1/5, 2/5, 3/5, 4/5. For nonuniformity, I offset each of the x and y interpolation parameters by a cosine function of the azumith and polar angle of the hair root on the scalp, and of the distance down the hair. I also varied the color of the hair by a cosine function of these same coordinates. Finally, I offset the final hair vertex positions out of the sphere if the hair vertex was in the sphere.
I did not try the static links approach mentioned in the paper, because I did not model a hairstyle; there was no "style" to preserve.
I made a movie [6] from my simulation, which incorporates the aforementioned techniques (plays in Windows Media Player, and VLC [7] on Mac and Linux). See encoding details for information on how the movie was made. I annotated some screenshots from the movie:
As you can see, I did not focus on rendering or modeling, so the head looks like a disco ball and the hair is a flat yellow color.
I encountered only one major problem: I could not get angular springs to work. When I tried to create torsional springs at every joint, one torsional spring would invariably bend too much, which would cause the two adjacent springs to see large angles and thus apply large spring forces. Thus if I tried to keep the hair in a neutral position with angular springs, the hair would always degenerate into a tangle of oscillating whip-like hairs. I could decrease the spring constant until this effect did not occur, but then the spring forces would not be sufficient to keep the hair in its initial position. One solution to this is to not use angular springs: instead, use static links, or have straight hair and render curls, as the authors suggested. Another solution might be to use smarter angular motors (with a force more complex than F = kx) or a PID [8]. These later alternatives sound rather complex.
For future work, I would want to actually model a hairstyle and implement static links to keep the hairstyle in place.